Quantum Computing Algorithms: Unlocking the Power of Quantum Mechanics

Quantum computing represents a revolutionary leap in computation, promising to solve problems that are currently intractable for classical computers. At the heart of this revolution are quantum computing algorithms, which leverage the principles of quantum mechanics to perform computations in fundamentally new ways. This article explores the world of quantum computing algorithms, delving into their theoretical foundations, key algorithms, and potential applications across various fields.

Basics of Quantum Computing

To understand quantum computing algorithms, it’s essential first to grasp the basics of quantum computing itself.

Qubits and Superposition

Unlike classical bits, which are either 0 or 1, quantum bits (qubits) can exist in a superposition of states. A qubit is represented as |ψ⟩ = α|0⟩ + β|1⟩, where α and β are complex numbers, and |α|^2 + |β|^2 = 1. This property allows quantum computers to process a vast amount of information simultaneously.

Entanglement

Entanglement is a quantum phenomenon where the state of one qubit becomes correlated with the state of another, regardless of the distance separating them. This correlation enables qubits to perform coordinated operations that are not possible with classical bits.

Quantum Gates and Circuits

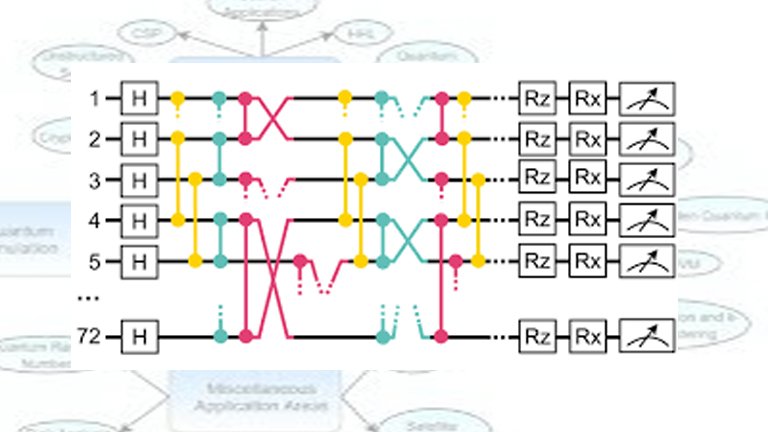
Quantum gates manipulate qubits and are the building blocks of quantum circuits, analogous to classical logic gates. Quantum gates, such as the Hadamard (H), Pauli-X, Pauli-Y, Pauli-Z, and Controlled-NOT (CNOT) gates, perform operations on qubits, enabling the implementation of quantum algorithms.

Measurement

Measurement in quantum computing collapses a qubit’s superposition state to a definite state (0 or 1) based on its probability amplitudes. The result of a quantum computation is probabilistic, and repeated measurements may be necessary to obtain a high-confidence answer.

Key Quantum Computing Algorithms

Quantum computing algorithms exploit the unique properties of qubits to achieve computational advantages over classical algorithms. Some of the most notable quantum algorithms include Shor’s algorithm, Grover’s algorithm, the Quantum Fourier Transform (QFT), and the Variational Quantum Eigensolver (VQE).

Shor’s Algorithm

Developed by Peter Shor in 1994, Shor’s algorithm efficiently factors large integers, a problem that underpins the security of many classical cryptographic systems like RSA. Classical factoring algorithms have exponential time complexity, but Shor’s algorithm can factor integers in polynomial time.

Algorithm Overview

1. Quantum Fourier Transform: Shor’s algorithm relies on the QFT to find the period of a function related to the integer to be factored.
2. Modular Exponentiation: The algorithm computes modular exponentiation in a quantum superposition, exploiting the parallelism of quantum computation.
3. Period Finding: By measuring the quantum state, the algorithm extracts the period of the function.
4. Classical Post-Processing: The period is used in classical computations to find the factors of the integer.

Shor’s algorithm’s ability to break RSA encryption highlights the transformative potential of quantum computing in cryptography.

Grover’s Algorithm

Developed by Lov Grover in 1996, Grover’s algorithm provides a quadratic speedup for unstructured search problems. While classical search algorithms require O(N) time to search an unsorted database of N items, Grover’s algorithm requires only O(√N) time.

Algorithm Overview

1. Superposition: The algorithm starts by placing the qubits in an equal superposition of all possible states.
2. Oracle Query: A quantum oracle marks the solution states by inverting their amplitudes.
3. Amplitude Amplification: The amplitudes of the marked states are increased while those of non-marked states are decreased.
4. Iteration: Steps 2 and 3 are repeated √N times to amplify the probability of measuring the correct solution.

Grover’s algorithm is particularly useful for database search, optimization problems, and cryptanalysis.

Quantum Fourier Transform (QFT)

The Quantum Fourier Transform (QFT) is the quantum analog of the classical discrete Fourier transform (DFT), and it plays a crucial role in many quantum algorithms, including Shor’s algorithm.

Algorithm Overview

1. Initialization: The qubits are initialized in a superposition state.
2. Hadamard Transform: The Hadamard gate is applied to each qubit, creating superpositions.
3. Controlled Phase Shifts: Controlled phase shift gates are applied to create the desired phase relationships between qubits.
4. Reversal of Qubit Order: The order of qubits is reversed to complete the transform.

The QFT enables efficient phase estimation, which is fundamental to algorithms like Shor’s and quantum phase estimation.

Variational Quantum Eigensolver (VQE)

The Variational Quantum Eigensolver (VQE) is a hybrid quantum-classical algorithm used to find the ground state energy of a quantum system. It is particularly suited for quantum chemistry and material science applications.

Algorithm Overview

1. Ansatz Preparation: A parameterized quantum circuit (ansatz) is prepared to represent the trial wave function.
2. Energy Measurement: The quantum computer measures the energy of the trial wavefunction for different parameter values.
3. Classical Optimization: A classical optimizer adjusts the parameters to minimize the measured energy.
4. Iteration: Steps 2 and 3 are iterated until the ground state energy is found.

VQE leverages the strengths of both quantum and classical computation to solve complex eigenvalue problems.

Advanced Quantum Algorithms

Beyond the foundational algorithms, advanced quantum algorithms are being developed to tackle a wide range of problems in cryptography, optimization, machine learning, and more.

Quantum Phase Estimation

Quantum phase estimation is a fundamental algorithm that underlies many other quantum algorithms, including Shor’s algorithm and quantum simulations.

Algorithm Overview

1. Initialization: A quantum register is initialized in a superposition state.
2. Controlled Unitary Operations: Controlled unitary operations are applied to entangle the phase information with the register.
3. Inverse QFT: The inverse Quantum Fourier Transform is applied to extract the phase information.
4. Measurement: The quantum register is measured to obtain the phase estimate.

Quantum phase estimation enables precise determination of eigenvalues and is crucial for solving problems in quantum chemistry and physics.

Quantum Approximate Optimization Algorithm (QAOA)

The Quantum Approximate Optimization Algorithm (QAOA) is designed to solve combinatorial optimization problems, such as the Max-Cut problem and traveling salesman problem.

Algorithm Overview

1. Initialization: The qubits are initialized in a superposition of all possible states.
2. Mixer and Cost Hamiltonians: The algorithm alternates between applying the mixer Hamiltonian and the cost Hamiltonian to evolve the quantum state.
3. Measurement: The final quantum state is measured to obtain the approximate solution.

QAOA leverages quantum parallelism to explore the solution space efficiently, offering potential speedups for optimization problems.

Quantum Machine Learning Algorithms

Quantum machine learning algorithms aim to enhance classical machine learning techniques by exploiting quantum parallelism and entanglement.

Quantum Support Vector Machine (QSVM)

The Quantum Support Vector Machine (QSVM) uses quantum computing to perform kernel-based classification more efficiently than classical SVMs.

Algorithm Overview

1. Quantum Feature Mapping: Classical data is mapped to a higher-dimensional quantum feature space.
2. Quantum Kernel Evaluation: The quantum computer evaluates the inner product of the quantum feature vectors.
3. Training: The support vectors are determined using classical optimization techniques.
4. Classification: New data points are classified based on the quantum kernel.

QSVM offers potential speedups for high-dimensional data classification tasks.

Quantum Principal Component Analysis (QPCA)

Quantum Principal Component Analysis (QPCA) performs dimensionality reduction on quantum data more efficiently than classical PCA.

Algorithm Overview

1. Covariance Matrix Preparation: The quantum computer prepares the covariance matrix of the data.
2. Quantum Phase Estimation: Quantum phase estimation is used to determine the eigenvalues and eigenvectors of the covariance matrix.
3. Measurement: The principal components are measured and extracted.

QPCA enables efficient analysis of large quantum datasets, providing insights into their underlying structure.

Applications of Quantum Computing Algorithms

Quantum computing algorithms have the potential to revolutionize various fields, from cryptography and optimization to machine learning and material science.

Cryptography

Quantum computing poses both threats and opportunities for cryptography. While algorithms like Shor’s threaten classical encryption methods, quantum cryptography offers new secure communication protocols.

Breaking Classical Cryptography

Shor’s algorithm can break widely used cryptographic systems like RSA and ECC by efficiently factoring large integers and computing discrete logarithms.

Quantum Key Distribution (QKD)

QKD leverages quantum mechanics to enable secure key exchange. Protocols like BB84 and E91 offer provable security based on the principles of quantum mechanics.

Optimization

Quantum algorithms like QAOA and Grover’s algorithm offer potential speedups for solving complex optimization problems.

Supply Chain Optimization

Quantum algorithms can optimize supply chain logistics, reducing costs and improving efficiency by finding optimal routes and schedules.

Financial Portfolio Optimization

Quantum computing can enhance financial portfolio optimization by efficiently exploring the vast solution space of possible asset allocations.

Machine Learning

Quantum machine learning algorithms promise to accelerate data analysis and improve the performance of classical machine learning techniques.

Drug Discovery

Quantum algorithms can model complex molecular interactions more accurately, speeding up the drug discovery process and leading to the development of new pharmaceuticals.

Image and Speech Recognition

Quantum-enhanced machine learning algorithms can improve the accuracy and efficiency of image and speech recognition systems, enabling more advanced AI applications.

Material Science

Quantum simulations can provide insights into the properties of new materials, leading to the development of advanced materials with unique properties.

Superconductors

Quantum algorithms can model the behavior of superconductors at the quantum level, aiding in the discovery of materials with higher critical temperatures.

Catalysts

Quantum simulations can identify and optimize catalysts for chemical reactions, leading to more efficient industrial processes and renewable energy solutions.

Challenges and Future Directions

While quantum computing algorithms hold immense promise, several challenges must be addressed to realize their full potential.

Hardware Limitations

Current quantum hardware is limited by qubit coherence times, gate fidelities, and error rates. Developing scalable, fault-tolerant quantum computers is essential for practical implementations of advanced quantum algorithms.

Error Correction

Quantum error correction is crucial for maintaining the integrity of quantum computations. Techniques like the surface code and topological qubits are being explored to achieve fault-tolerant quantum computing.

Algorithm Development

Developing new quantum algorithms and improving existing ones is an ongoing research challenge. Hybrid quantum-classical algorithms and variational approaches offer promising directions for leveraging near-term quantum hardware.

Standardization and Benchmarking

Establishing standards and benchmarks for quantum algorithms is essential for evaluating their performance and comparing them with classical counterparts. Initiatives like the Quantum Algorithm Zoo and QBench provide frameworks for this purpose.

Conclusion

Quantum computing algorithms represent a transformative advancement in computation, offering the potential to solve problems that are currently beyond the reach of classical computers. From Shor’s algorithm and Grover’s algorithm to advanced techniques like QAOA and VQE, these algorithms leverage the unique properties of quantum mechanics to achieve unprecedented computational power. As quantum hardware continues to improve and new algorithms are developed, the applications of quantum computing will expand, impacting fields as diverse as cryptography, optimization, machine learning, and material science. Despite the challenges, the future of quantum computing holds immense promise, heralding a new era of technological innovation and discovery.